
Le cycle de l'eau H2O
Sans un cycle, l'eau ne se renouvellerait pas sur Terre empêchant toute formation d'océans et donc de milieu aquatique susceptible d'accueillir de la vie .
Un renouvellement de l'eau est alors nécessaire passant par une série de transformations dont nous allons en voir les principaux détails .
1 ) Généralités
2 ) Masse critique d'une gouttelette d'eau pour
qu'elle s'échappe dans l'espace
3 ) Applications numériques

Sous l'effet des rayons du soleil, de la vapeur d'eau se forme ; or la gravité de la Terre est faible : l'eau gazeuse ( gaz dihydrogène H2 + gaz Oxygène O : gaz légers ) s'élève facilement dans l'air .De l'air chaud et humide se forme alors : c'est l'évaporation .
Le volume d'air ( ajout du gaz eau ) augmente alors sensiblement .
Or, si nous considérons les gaz de l'atmosphère comme des gaz parfaits, nous avons :
PV = nRT
P : pression du gaz .
V : volume du gaz .
n : nombre de moles du gaz .
R : constante des gaz parfaits qui vaut 8,31 J / K / mol .
T : température du gaz .
D'où
P = ( nRT ) / V
A T constante, n constante, R constante ( par définition ), la pression du gaz diminue ; une dépression se crée alors : la vapeur d'eau rencontre ensuite des noyaux de condensation ( grains, poussières ) autour desquels elle s'enroule ; des mouvements de rotation ont alors lieu faisant que des gouttelettes d'eau à l'état liquide se forme .
Un ensemble de gouttelettes d'eau abouti à la formation d'un nuage en rencontrant de l'air froid et sec : c'est la condensation .
De plus, les gouttelettes d'eau ont une vitesse de chute variant entre 0,1 m / s ( brouillard ) et 9 m / s ( Averse ) : nous verrons par la suite comment déterminer ces vitesses .
Or, la pression atmosphérique est le poids d'une colonne d'air sur une surface donnée ; plus l'altitude est élevée, plus la colonne d'air devient légère car la gravité fait que les gaz les plus légers ne sont pas "plaquées" au sol ; l'air va ainsi des hautes pressions vers les basses pressions formant par conséquent des mouvements ascendants de l'air : les vitesses de chute des gouttelettes d'eau sont alors facilement compensées par les mouvements ascendants de l'air ( entre 10 km / h et 100 km / h voire plus tout dépend de la situation météorologique ) .
2 ) Masse critique d'une gouttelette d'eau pour qu'elle s'échappe dans l'espace
Mais la masse des gouttelettes d'eau reste faible dans l'ensemble ; en effet, en appliquant le principe fondamental de la dynamique au système { gouttelette d'eau }, nous avons :
SF(ext)=m(c)a
SF(ext) : somme des forces extérieures au système .
m(c) : masse critique d'une gouttelette d'eau isolée sur Terre pour qu'elle tombe sous l'effet de la gravité à une température donnée .
a : accélération de la gouttelette d'eau .
Seule la force gravitationnelle ( notée F ) s'exerce sur la gouttelette d'eau .
D'où
F = m(c)a
GM(T)m(c)/(R+r)²=m(c)a ( 1 )
M(T) : masse de la Terre .
R : rayon de la Terre .
G : constante de gravitation universelle qui vaut 6,67.10^-11 .
La gouttelette d'eau est animée d'un mouvement vertical : la composante tangentielle de l'accélération est donc égale à zéro .
D'où
a = V(c)²/r
V(c) : vitesse de la gouttelette d'eau .
r : altitude à laquelle se trouve la gouttelette d'eau .
Détermination de V(c) :
La gouttelette d'eau est soumise à la résultante des efforts de pression comme dans le schéma ci-dessous :
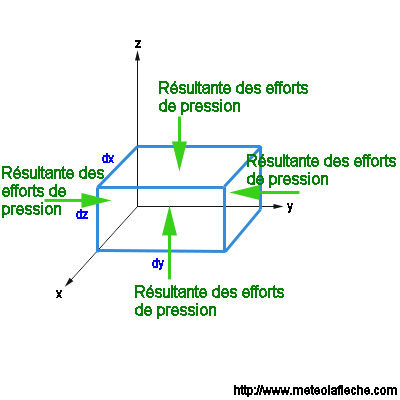
D'où
P(z) + r(z)gz = cte Loi de l'hydrostatique
P(z) : pression atmosphérique à l'altitude z .
r(z) : densité de probabilité de la gouttelette d'eau à l'altitude z .
g : intensité du champ de pesanteur qui vaut 9,81 m / s² .
De plus,
F(p) = SP(z)
F(p) : force de pression exercée sur la gouttelette d'eau négligeable devant la force de gravitation .
S : surface de la gouttelette d'eau .
A T constante, g constante,
PV = n(z)k(B)T ( 2 )
n(z) : nombre de moles à l'altitude z .
k(B) : constante de Boltzmann qui vaut 1,38.10^-23 J / K .
D'où
dP(z) = -P(z) dz m(c) g / ( KT )
P(z) = P(0)exp[ - m(c)gz / ( KT ) ] en intégrant par rapport à z
KT : agitation thermique .
mgz : énergie potentielle .
A T fixée, chaque molécule de l'air est répartie sur un niveau d'énergie de manière aléatoire provoquant un désordre du système { gouttelette d'eau } .Les molécules de l'air des différents niveaux d'énergie sont reliées entre elles formant une distribution : la distribution de Boltzmann .
Or, la probabilité que la gouttelette d'eau appartienne au niveau d'énergie ( z, z+dz ) est notée dp(z) telle que :
dp(z) = p(z)dz
p(z) : densité de probabilité que la gouttelette d'eau appartienne au niveau d'énergie ( z, z+dz ) .
D'après ( 2 ),
n(z) = PV / ( k(B)T )
D'où
dp(z)=n(z)dz / N
N : nombre de gouttelettes d'eau à l'altitude z .
dp(z)=n(0)exp(-m(c)gz/( k(B)T ) ) / N
D'où
p(z)=p(0)exp(-m(c)gz/( k(B)T ) )
Au niveau de la distribution des composantes de V, nous avons par conséquent :
dP(V(c)) = ( V(c) / Z ) exp [ -E(c) / ( k(B)T ) ]dv
Z : fonction de partition du système { gouttelette d'eau } qui est une fonction de la température T et de V(c), et qui englobe les propriétés statistiques du système à l'état thermodynamique .
E(c) : énergie cinétique du système { gouttelette d'eau } .
dv=dv(x)dv(y)dv(z) .
D'où
dP(V(c)) = [ m(c) / 2pk(B)T ]^(1/2) exp [ -(1/2)m(c)v² / ( k(B)T ) ]dv
En intégrant par rapport à v, nous obtenons
P(V(c))dv=[ m(c) / 2pk(B)T ]^(3/2) 4pv² exp [ -(1/2)m(c)v² / ( k(B)T ) ]dv Distribution de Maxwell
D'où
dP(V(c))/dv = -v^3 m(c) / k(B)T + 2v
Or, P(V) est constante à v=V .
D'où
dP(V(c))/dv = -v^3 m(c) / k(B)T + 2v = 0
Nous en déduisons
V(c) = { 2k(B)T / [ m(c) ] }^(1/2) ( 3 )
Détermination de m(c) :
En incorporant l'expression de ( 3 ) dans l'expression de ( 1 ), nous obtenons la masse critique d'une gouttelette d'eau isolée à une température T donnée :
m(c) = [ 2k(B)T( R + r )² ] / [ G M(T) r ]
Par exemple, pour le gaz hydrogène ( gaz le plus léger sur Terre ) à T = 300 K et situé à r = 1 km, la masse critique de ce gaz serait de 1.3.10^-27 g .
Concernant l'eau liquide, nous avons :
m(c) = n(c) M(eau)
n(c) : quantité de matière de la gouttelette d'eau .
M(eau) : masse molaire de la gouttelette d'eau .
Considérons l'eau comme un gaz parfait, ce qui donne :
n(c) = P(eau)V(eau) / RT(eau)
P(eau) : pression de l'eau liquide .
V(eau) : volume de l'eau liquide .
T(eau) : température de l'eau liquide .
D'où
m(c) = M(eau) P(eau)V(eau) / RT(eau)
De plus, nous assimilons la gouttelette d'eau à une sphère de rayon r(eau) tel que :
V(eau) = (4/3)p[r(eau)]^2
Le manque de cohésion entre les gouttelettes d'eau qui est dû à un volume d'air faible en altitude fait que r(eau) < 3 mm .
D'où
m(c) = [ 4 M(eau)P(eau)[r(eau)]^2 ] / [ 3RT(eau) ]
Nous trouvons selon le diamètre de la gouttelette d'eau ( assimilée à une sphère ) :
|
Diamètre de la goutte ( mm ) |
0,06 |
0,5 |
3 |
6 |
|
m(c) ( mg ) |
10^-7 |
6.10^-5 |
10^-4 |
7.10^-4 |
|
V(c) ( m / s ) |
0,1 |
2 |
8 |
9 |
Nous montrons ainsi que plus l'air est chaud, plus il peut contenir des particules d'eau .
Du coup, la plupart des gouttelettes d'eau continue à s'élever dans l'atmosphère passant de l'état liquide à l'état solide tout en grossissant : c'est l'effet Bergeron .
Les cristaux de glace formés finissent par avoir une masse si élevée que les mouvements ascendants générés par une différence de pression entre le sol ( pression atmosphérique élevée ) et l'altitude ( pression atmosphérique nettement plus faible ) ne sont plus suffisamment intenses pour les empêcher de tomber au sol .
Dans une situation météorologique "classique", les cristaux de glace, en chutant à une vitesse faible, rencontrent à nouveau de l'air chaud et humide et/ou de l'air chaud et sec en grande quantité : la pression atmosphérique augmente à nouveau ; d'après le diagramme de Clapeyron, il y a sublimation ; certains cristaux de glace rencontrent des gouttelettes d'eau et s'agglutinent entre elles : c'est l'effet de coalescence et de captation .